TL;DR: In RLHF, there’s stress between the reward studying section, which makes use of human desire within the type of comparisons, and the RL fine-tuning section, which optimizes a single, non-comparative reward. What if we carried out RL in a comparative means?
Determine 1:
This diagram illustrates the distinction between reinforcement studying from absolute suggestions and relative suggestions. By incorporating a brand new part – pairwise coverage gradient, we are able to unify the reward modeling stage and RL stage, enabling direct updates primarily based on pairwise responses.
Massive Language Fashions (LLMs) have powered more and more succesful digital assistants, comparable to GPT-4, Claude-2, Bard and Bing Chat. These techniques can reply to advanced consumer queries, write code, and even produce poetry. The approach underlying these superb digital assistants is Reinforcement Studying with Human Suggestions (RLHF). RLHF goals to align the mannequin with human values and eradicate unintended behaviors, which might typically come up as a result of mannequin being uncovered to a big amount of low-quality information throughout its pretraining section.
Proximal Coverage Optimization (PPO), the dominant RL optimizer on this course of, has been reported to exhibit instability and implementation issues. Extra importantly, there’s a persistent discrepancy within the RLHF course of: regardless of the reward mannequin being skilled utilizing comparisons between varied responses, the RL fine-tuning stage works on particular person responses with out making any comparisons. This inconsistency can exacerbate points, particularly within the difficult language era area.
Given this backdrop, an intriguing query arises: Is it attainable to design an RL algorithm that learns in a comparative method? To discover this, we introduce Pairwise Proximal Coverage Optimization (P3O), a way that harmonizes the coaching processes in each the reward studying stage and RL fine-tuning stage of RLHF, offering a passable answer to this situation.
Background
Determine 2:
An outline of the three levels of RLHF from an OpenAI weblog put up. Observe that the third stage falls beneath Reinforcement Studying with Absolute Suggestions as proven on the left facet of Determine 1.
In conventional RL settings, the reward is specified manually by the designer or supplied by a well-defined reward perform, as in Atari video games. Nonetheless, to steer a mannequin towards useful and innocent responses, defining a great reward will not be easy. RLHF addresses this drawback by studying the reward perform from human suggestions, particularly within the type of comparisons, after which making use of RL to optimize the discovered reward perform.
The RLHF pipeline is split into a number of levels, detailed as follows:
Supervised Tremendous-Tuning Stage: The pre-trained mannequin undergoes the utmost chance loss on a top quality dataset, the place it learns to reply to human queries via mimicking.
Reward Modeling Stage: The SFT mannequin is prompted with prompts (x) to provide pairs of solutions (y_1,y_2sim pi^{textual content{SFT}}(yvert x)). These generated responses kind a dataset. The response pairs are introduced to human labellers who categorical a desire for one reply over the opposite, denoted as (y_w succ y_l). A comparative loss is then used to coach a reward mannequin (r_phi):
[mathcal{L}_R = mathbb{E}_{(x,y_l,y_w)simmathcal{D}}log sigmaleft(r_phi(y_w|x)-r_phi(y_l|x)right)]
RL Tremendous-Tuning Stage: The SFT mannequin serves because the initialization of this stage, and an RL algorithm optimizes the coverage in the direction of maximizing the reward whereas limiting the deviation from the preliminary coverage. Formally, that is completed via:
[max_{pi_theta}mathbb{E}_{xsim mathcal{D}, ysim pi_theta(cdotvert x)}left[r_phi(yvert x)-beta D_{text{KL}}(pi_theta(cdotvert x)Vert pi^{text{SFT}}(cdotvert x))right]]
An inherent problem with this method is the non-uniqueness of the reward. For example, given a reward perform (r(yvert x)), a easy shift within the reward of the immediate to (r(yvert x)+delta(x)) creates one other legitimate reward perform. These two reward capabilities end in the identical loss for any response pairs, however they differ considerably when optimized in opposition to with RL. In an excessive case, if the added noise causes the reward perform to have a wide range, an RL algorithm is likely to be misled to extend the chance of responses with larger rewards, although these rewards might not be significant. In different phrases, the coverage is likely to be disrupted by the reward scale data within the immediate (x), but fails to be taught the helpful half – relative desire represented by the reward distinction. To handle this situation, our goal is to develop an RL algorithm that’s invariant to reward translation.
Derivation of P3O
Our thought stems from the vanilla coverage gradient (VPG). VPG is a broadly adopted first-order RL optimizer, favored for its simplicity and ease of implementation. In a contextual bandit (CB) setting, the VPG is formulated as:
[nabla mathcal{L}^{text{VPG}} = mathbb{E}_{ysimpi_{theta}} r(y|x)nablalogpi_{theta}(y|x)]
By way of some algebraic manipulation, we are able to rewrite the coverage gradient in a comparative kind that includes two responses of the identical immediate. We title it Pairwise Coverage Gradient:
[mathbb{E}_{y_1,y_2simpi_{theta}}left(r(y_1vert x)-r(y_2vert x)right)nablaleft(logfrac{pi_theta(y_1vert x)}{pi_theta(y_2vert x)}right)/2]
In contrast to VPG, which immediately depends on absolutely the magnitude of the reward, PPG makes use of the reward distinction. This permits us to bypass the aforementioned situation of reward translation. To additional increase efficiency, we incorporate a replay buffer utilizing Significance Sampling and keep away from massive gradient updates through Clipping.
Significance sampling: We pattern a batch of responses from the replay buffer which include responses generated from (pi_{textual content{previous}}) after which compute the significance sampling ratio for every response pair. The gradient is the weighted sum of the gradients computed from every response pair.
Clipping: We clip the significance sampling ratio in addition to the gradient replace to penalize excessively massive updates. This system allows the algorithm to trade-off KL divergence and reward extra effectively.
There are two other ways to implement the clipping approach, distinguished by both separate or joint clipping. The ensuing algorithm is known as Pairwise Proximal Coverage Optimization (P3O), with the variants being V1 or V2 respectively. Yow will discover extra particulars in our authentic paper.
Analysis
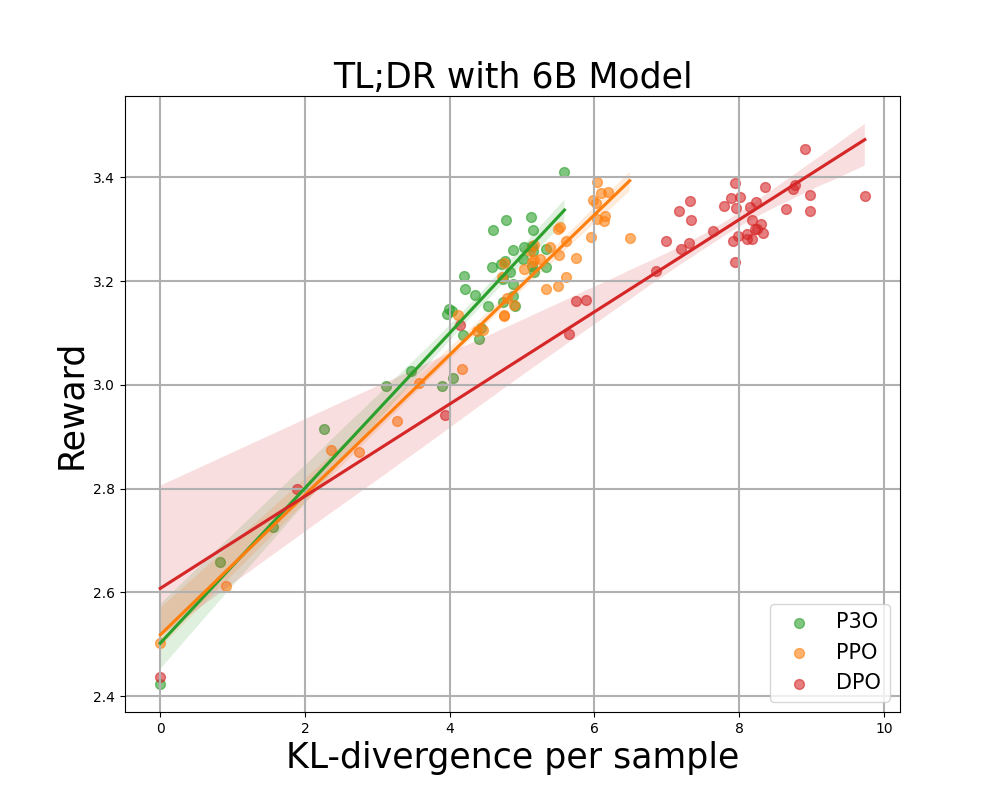
Determine 3:
KL-Reward frontier for TL;DR, each sequence-wise KL and reward are averaged over 200 take a look at prompts and computed each 500 gradient steps. We discover {that a} easy linear perform suits the curve effectively. P3O has the very best KL-Reward trade-off among the many three.
We discover two totally different open-ended textual content era duties, summarization and question-answering. In summarization, we make the most of the TL;DR dataset the place the immediate (x) is a discussion board put up from Reddit, and (y) is a corresponding abstract. For question-answering, we use Anthropic Useful and Innocent (HH), the immediate (x) is a human question from varied matters, and the coverage ought to be taught to provide an enticing and useful response (y).
We examine our algorithm P3O with a number of efficient and consultant approaches for LLM alignment. We begin with the SFT coverage skilled by most chance. For RL algorithms, we take into account the dominant method PPO and the newly proposed DPO. DPO immediately optimizes the coverage in the direction of the closed-form answer of the KL-constrained RL drawback. Though it’s proposed as an offline alignment methodology, we make it on-line with the assistance of a proxy reward perform.
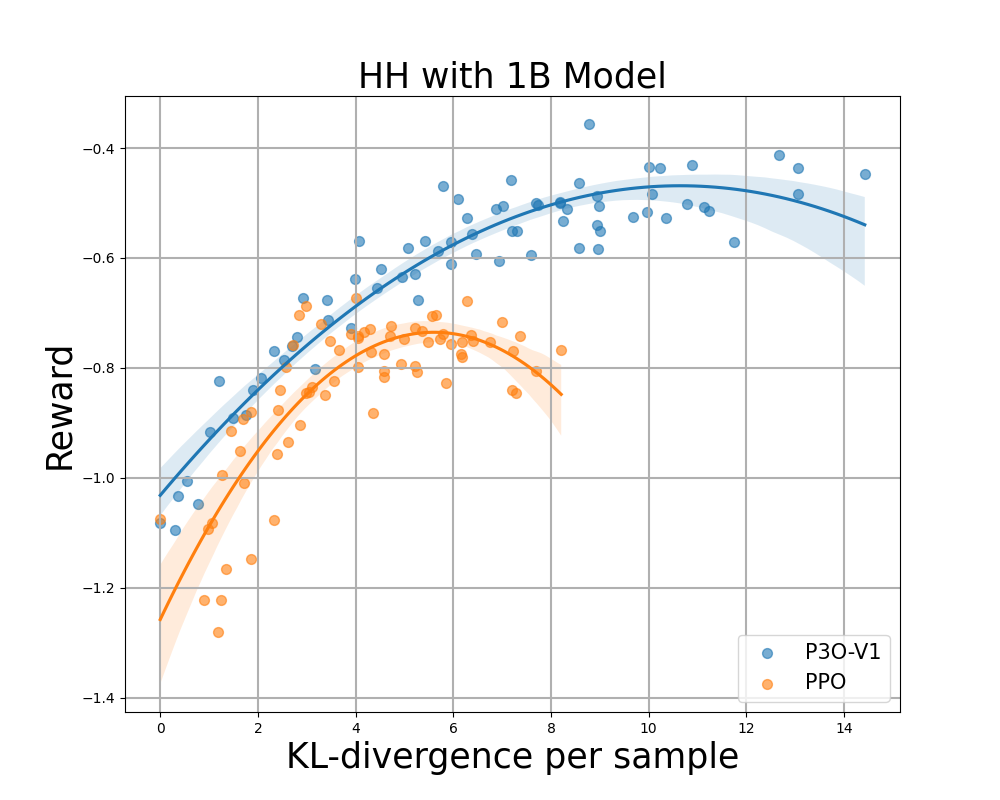
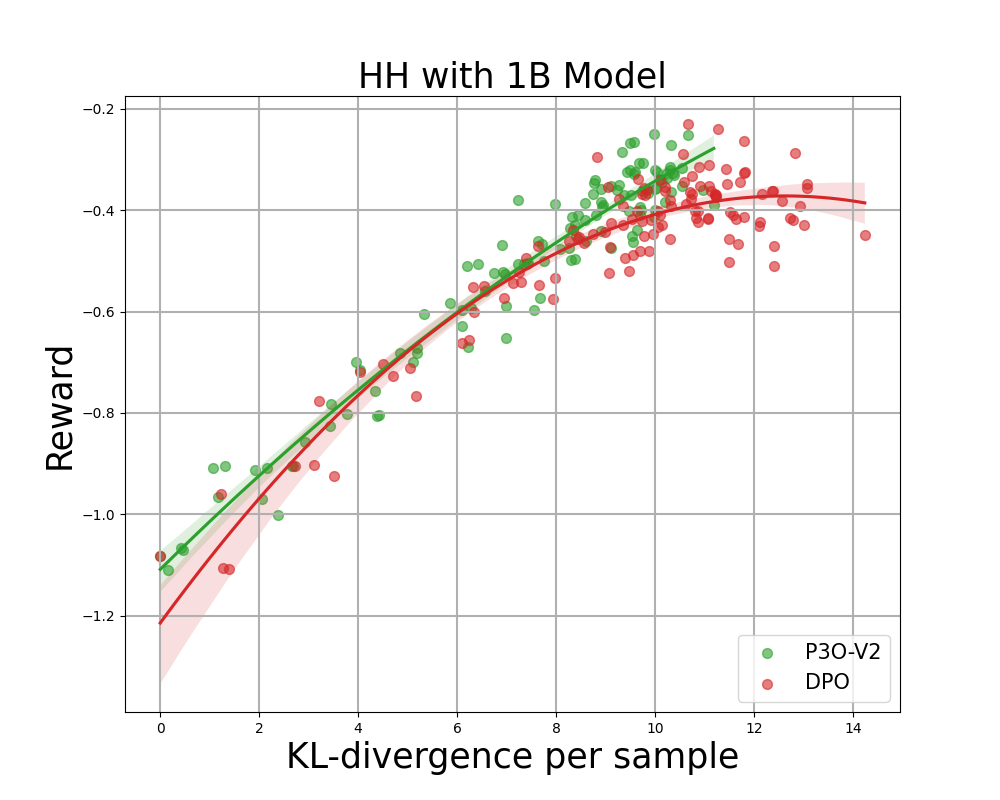
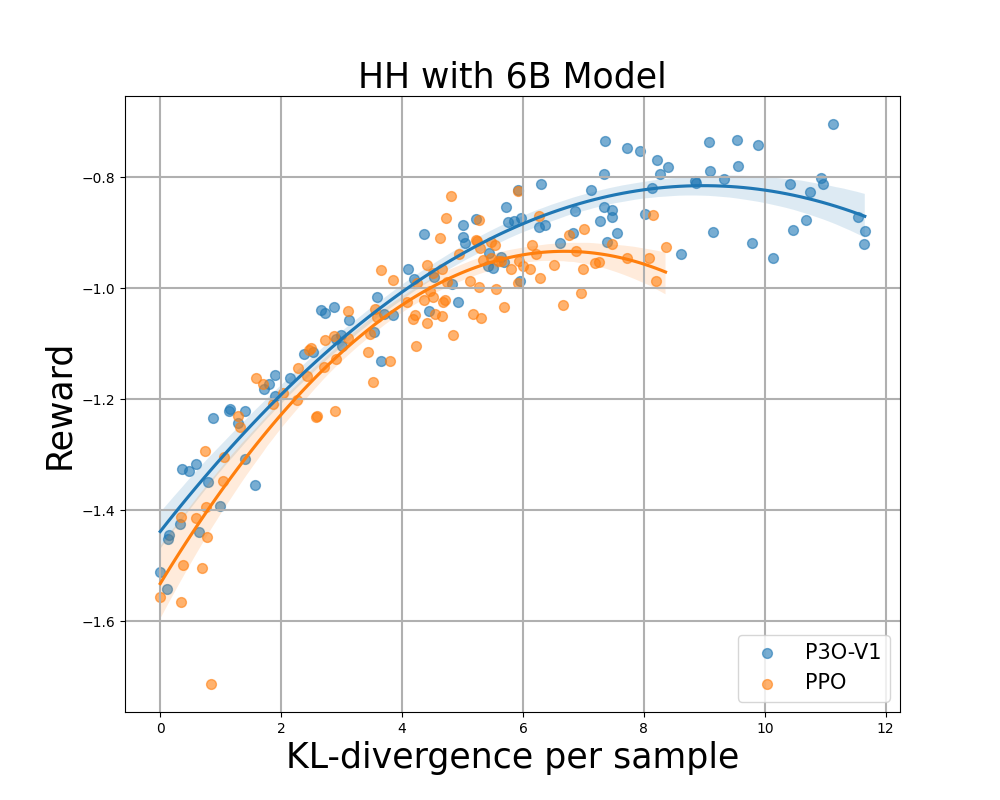
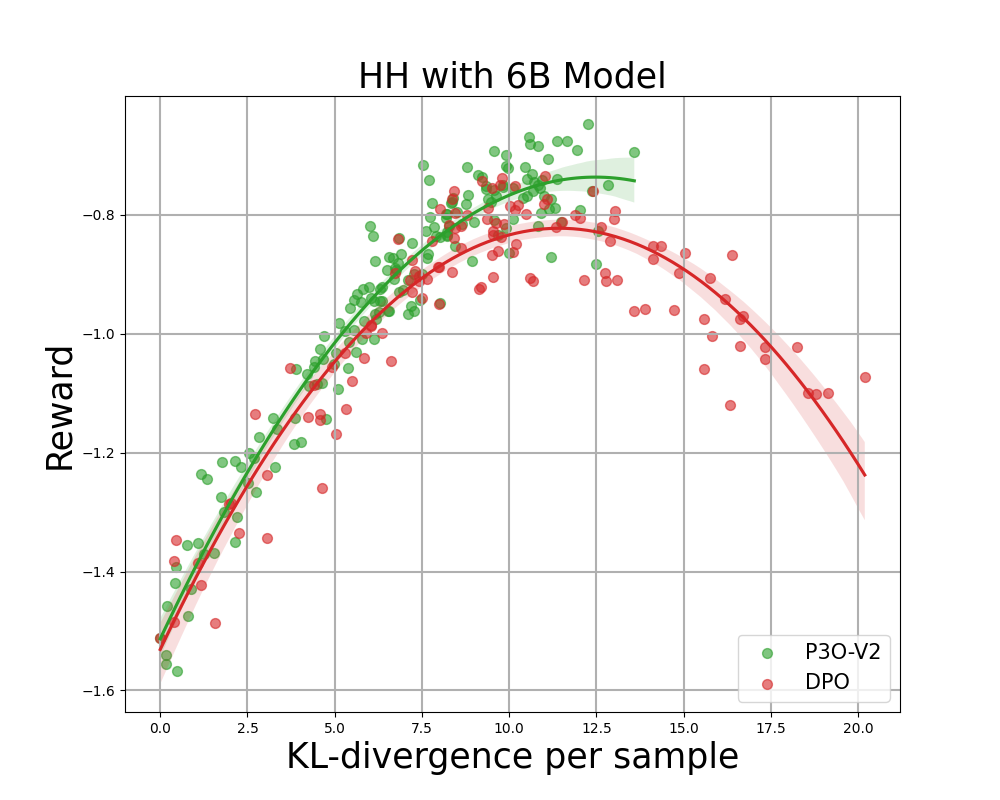
Determine 4:
KL-Reward frontier for HH, every level represents a median of outcomes over 280 take a look at prompts and calculated each 500 gradient updates. Left two figures examine P3O-V1 and PPO with various base mannequin sizes; Proper two figures examine P3O-V2 and DPO. Outcomes displaying that P3O cannot solely obtain larger reward but additionally yield higher KL management.
Deviating an excessive amount of from the reference coverage would lead the web coverage to chop corners of the reward mannequin and produce incoherent continuations, as identified by earlier works. We’re focused on not solely the effectively established metric in RL literature – the reward, but additionally in how far the discovered coverage deviates from the preliminary coverage, measured by KL-divergence. Subsequently, we examine the effectiveness of every algorithm by its frontier of achieved reward and KL-divergence from the reference coverage (KL-Reward Frontier). In Determine 4 and Determine 5, we uncover that P3O has strictly dominant frontiers than PPO and DPO throughout varied mannequin sizes.
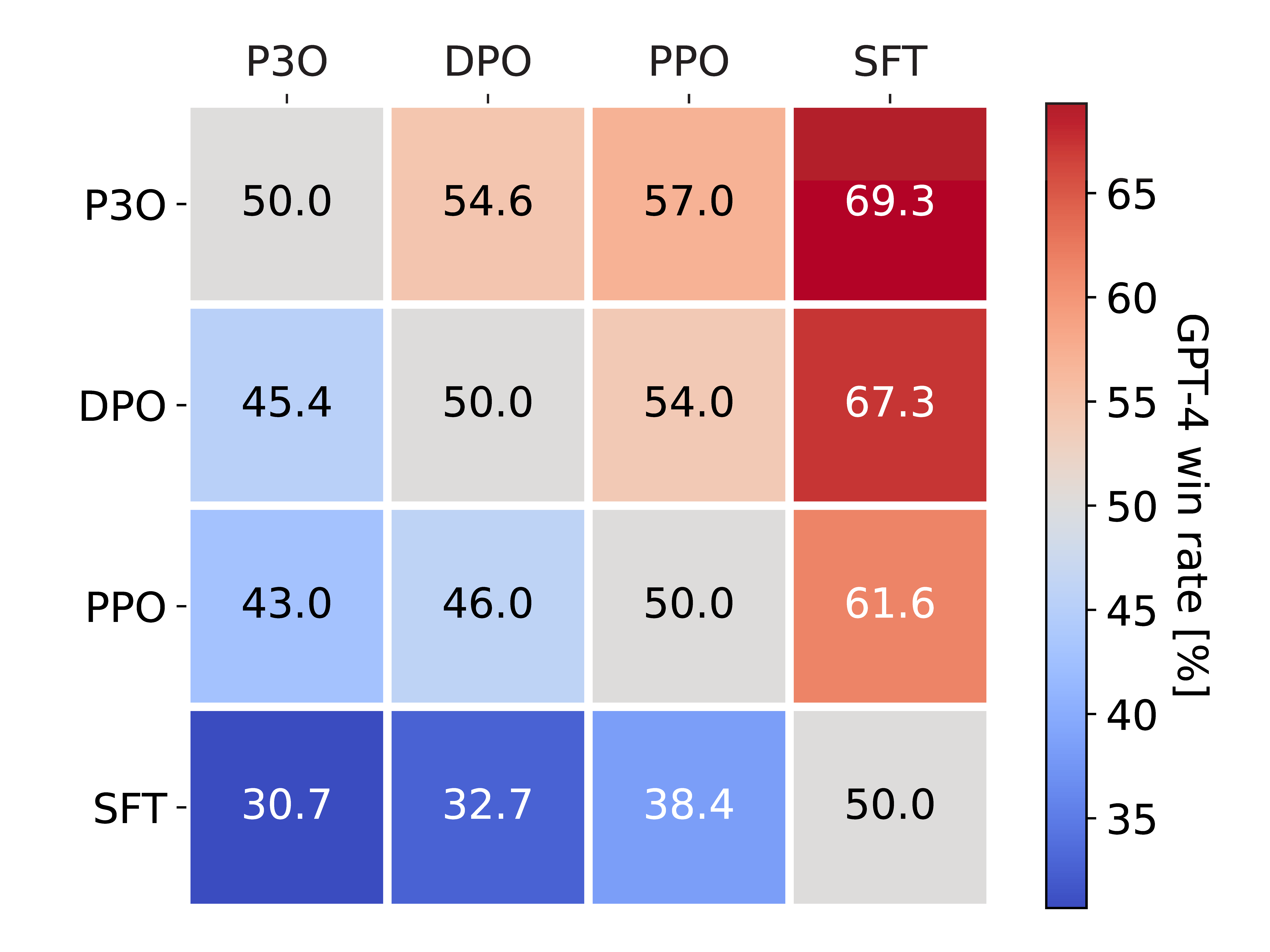
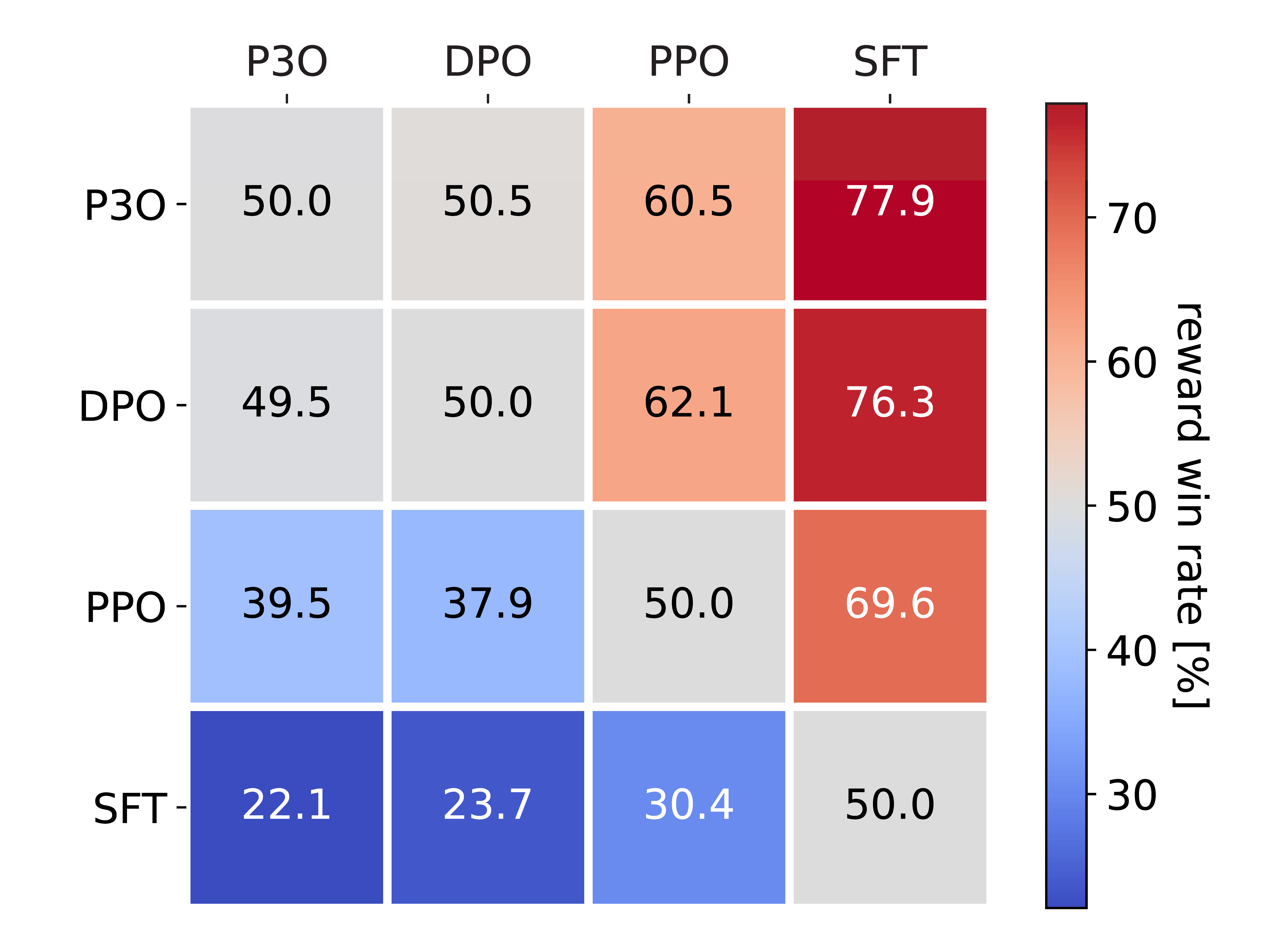
Determine 5:
Left determine shows the win price evaluated by GPT-4. Proper determine presents the win price primarily based on direct comparability of the proxy reward. Regardless of the excessive correlation between two figures, we discovered that the reward win price should be adjusted in response to the KL in an effort to align with the GPT-4 win price.
To immediately assess the standard of generated responses, we additionally carry out Head-to-Head Comparisons between each pair of algorithms within the HH dataset. We use two metrics for analysis: (1) Reward, the optimized goal throughout on-line RL, (2) GPT-4, as a trustworthy proxy for human analysis of response helpfulness. For the latter metric, we level out that earlier research present that GPT-4 judgments correlate strongly with people, with human settlement with GPT-4 usually related or larger than inter-human annotator settlement.
Determine 5 presents the excellent pairwise comparability outcomes. The typical KL-divergence and reward rating of those fashions is DPO > P3O > PPO > SFT. Though DPO marginally surpasses P3O in reward, it has a significantly larger KL-divergence, which can be detrimental to the standard of era. Consequently, DPO has a reward win price of 49.5% in opposition to P3O, however solely 45.4% as evaluated by GPT-4. In contrast with different strategies, P3O reveals a GPT-4 win price of 57.0% in opposition to PPO and 69.3% in opposition to SFT. This result’s in keeping with our findings from the KL-Reward frontier metric, affirming that P3O might higher align with human desire than earlier baselines.
Conclusion
On this weblog put up, we current new insights into aligning massive language fashions with human preferences through reinforcement studying. We proposed the Reinforcement Studying with Relative Suggestions framework, as depicted in Determine 1. Underneath this framework, we develop a novel coverage gradient algorithm – P3O. This method unifies the elemental rules of reward modeling and RL fine-tuning via comparative coaching. Our outcomes present that P3O surpasses prior strategies when it comes to the KL-Reward frontier in addition to GPT-4 win-rate.
BibTex
This weblog is predicated on our current paper and weblog. If this weblog evokes your work, please take into account citing it with:
@article{wu2023pairwise,
title={Pairwise Proximal Coverage Optimization: Harnessing Relative Suggestions for LLM Alignment},
writer={Wu, Tianhao and Zhu, Banghua and Zhang, Ruoyu and Wen, Zhaojin and Ramchandran, Kannan and Jiao, Jiantao},
journal={arXiv preprint arXiv:2310.00212},
yr={2023}
}